2 Error in triangulation systems

For optical triangulation systems, the accuracy of the range data depends on proper interpretation of imaged light reflections. The most common approach is to reduce the problem to one of finding the ``center'' of a one dimensional pulse, where the ``center'' refers to the position on the sensor which hopefully maps to the center of the illuminant. Typically, researchers have opted for a statistic such as mean, median or peak of the imaged light as representative of the center. These statistics give the correct answer when the surface is perfectly planar, but they are generally inaccurate whenever the surface perturbs the shape of the illuminant.

2.1 Geometric intuition

Perturbations of the shape of the imaged illuminant occur whenever:

• The surface reflectance varies.
• The surface geometry deviates from planarity.
• The light paths to the sensor are partially occluded.
• The surface is sufficiently rough to cause laser speckle.

In Figure 2, we give examples of how the first three circumstances result in range errors even for an ideal triangulation system with infinite sensor resolution and perfect calibration. For purposes of illustration, we omit the imaging optics of Figure 1 and treat the sensor as a one dimensional orthographic sensor. Further, we assume an illuminant of Gaussian cross-section, and we use the mean for determining the center of an imaged pulse. Figure 2a shows how a step reflectance discontinuity results in range points that do not lie on the surface. Figure 2b and 2c provide two examples of shape variations resulting in range errors. Note that in Figure 2c, the center of the illuminant is not even striking a surface. In this case, a measure of the center of the pulse results in a range value, when in fact the correct answer is to return no range value whatever. Finally, Figure 2d shows the effect of occluding the line of sight between the illuminated surface and the sensor. This range error is very similar to the error encountered in Figure 2c.

 

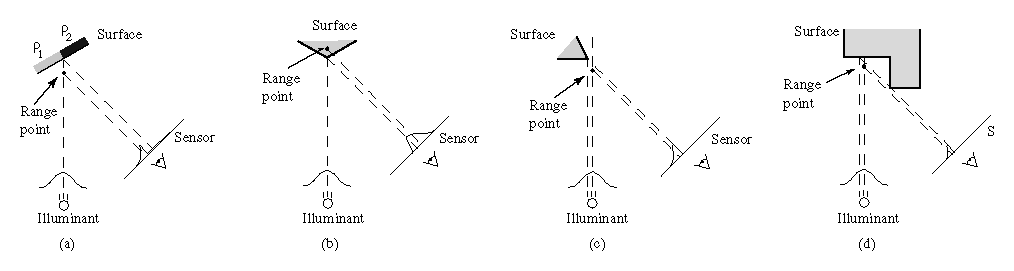
Figure 2: Range errors using traditional triangulation methods. (a) Reflectance discontinuity. (b) Corner. (c) Shape discontinuity with respect to the illumination. (d) Sensor occlusion. 

The fourth source of range error is laser speckle, which arises when coherent laser illumination bounces off of a surface that is rough compared to a wavelength [7]. The surface roughness introduces random variations in optical path lengths, causing a random interference pattern throughout space and at the sensor. The result is an imaged pulse with a noise component that affects the mean pulse detection, causing range errors even from a planar target.

2.2 Quantifying the error

To quantify the errors inherent in using mean pulse analysis, we have computed the errors introduced by reflectance and shape variations for an ideal triangulation system with a single Gaussian illuminant. We take the beam width, w, to be the distance between the beam center and the point of the irradiance profile, a convention common to the optics literature. We present the range errors in a scale invariant form by dividing all distances by the beam width. Figure 3 illustrates the maximum deviation from planarity introduced by scanning reflectance discontinuities of varying step magnitudes for varying triangulation angles. As the size of the step increases, the error increases correspondingly. In addition, smaller triangulation angles, which are desirable for reducing the likelihood of missing data due to sensor occlusions, actually result in larger range errors. This result is not surprising, as sensor mean positions are converted to depths through a division by , where is the triangulation angle, so that errors in mean detection translate to larger range errors for smaller triangulation angles.

Figure 4 shows the effects of a corner on range error, where the error is taken to be the shortest distance between the computed range data and the exact corner point. The corner is oriented so that the illumination direction bisects the corner's angle as shown in Figure 2b. As we might expect, a sharper corner results in greater compression of the left side of the imaged Gaussian relative to the right side, pushing the mean further to the right on the sensor and pushing the triangulated point further behind the corner. In this case, the triangulation angle has little effect as the division by is offset almost exactly by the smaller observed left/right pulse compression imbalance.

 
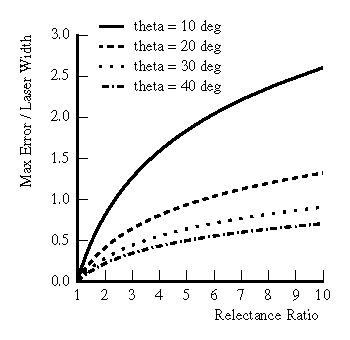
Figure 3: Plot of errors due to reflectance discontinuities for varying triangulation angles (theta). 

 
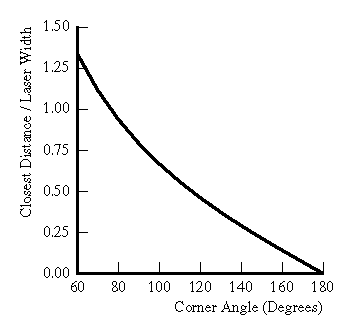
Figure 4: Plot of errors due to corners. 

One possible strategy for reducing these errors would be to decrease the width of the beam and increase the resolution of the sensor. However, diffraction limits prevent us from focusing the beam to an arbitrary width. The limits on focusing a Gaussian beam with spherical lenses are well known [15]. In recent years, Bickel, et al, [3] have explored the use of axicons (e.g., glass cones and other surfaces of revolution) to attain tighter focus of a Gaussian beam. The refracted beam, however, has a zeroth order Bessel function cross-section; i.e., it has numerous side-lobes of non-negligible irradiance. The influence of these side-lobes is not well-documented and would seem to complicate triangulation.