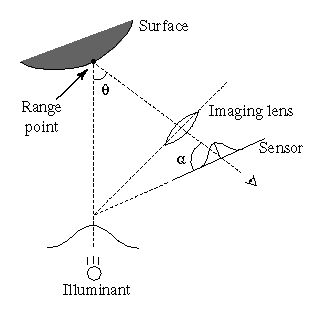
Figure 1: Optical triangulation geometry. The angle
Active optical triangulation is one of the most common methods for acquiring range data. Although this technology has been in use for over twenty years, its speed and accuracy has increased dramatically in recent years with the development of geometrically stable imaging sensors such as CCD's and lateral effect photodiodes. The range acquisition literature contains many descriptions of optical triangulation range scanners, of which we list a handful [2] [8] [10] [12] [14] [17] . The variety of methods differ primarily in the structure of the illuminant (typically point, stripe, multi-point, or multi-stripe), the dimensionality of the sensor (linear array or CCD grid), and the scanning method (move the object or move the scanner hardware).
Figure 1 shows a typical system configuration in two dimensions. The location of the center of the reflected light pulse imaged on the sensor corresponds to a line of sight that intersects the illuminant in exactly one point, yielding a depth value. The shape of the object is acquired by translating or rotating the object through the beam or by scanning the beam across the object.
The accuracy of optical triangulation methods hinges on the ability to locate the ``center'' of the imaged pulse at each time step. For optical triangulation systems that extract range from single imaged pulses at a time, variations in surface reflectance and shape result in systematic range errors. Several researchers have observed one or both of these accuracy limitations [4] [12] [16]. For the case of coherent illumination, the images of reflections from rough surfaces are also subject to laser speckle noise, introducing noise into the range data. Researchers have studied the effect of speckle on range determination and have indicated that it is a fundamental limit to the accuracy of laser range triangulation, though its effects can be reduced with well-known speckle reduction techniques [1] [5]. Mundy and Porter [12] attempt to correct for variations in surface reflectance by noting that two imaged pulses, differing in position or wavelength are sufficient to overcome the reflectance errors, though some restrictive assumptions are necessary for the case of differing wavelengths. Kanade, et al, [11] describe a rangefinder that finds peaks in time for a stationary sensor with pixels that view fixed points on an object. This method of peak detection is very similar to the one presented in this paper for solving some of the problems of optical triangulation; however, the authors in [11] do not indicate that their design solves or even addresses these problems. Further, we show that the principle generalizes to other scanning geometries.
In the following sections, we first show how range errors arise with traditional triangulation techniques. In section 3, we show that by analyzing the time evolution of structured light reflections, a process we call spacetime analysis, we can overcome the accuracy limitations caused by shape and reflectance variations. Experimental evidence also indicates that laser speckle behaves in a manner that allows us to reduce its distorting effect as well.
In sections 4 and 5, we describe our hardware and software implementation of the spacetime analysis using a commercial scanner and a video digitizer, and we demonstrate a significant improvement in range accuracy. Finally, in section 6, we conclude and describe future directions.

Figure 1: Optical
triangulation geometry. The angle ![]() is the triangulation angle
while
is the triangulation angle
while ![]() is the tilt of the sensor plane needed to keep the
laser plane in focus.
is the tilt of the sensor plane needed to keep the
laser plane in focus.