Tamara Munzner
1
The Geometry Center, University of Minnesota
2
Paul Burchard
3
Department of Mathematics, University of Utah
4
We visualize the structure of sections of the World Wide Web by constructing graphical representations in 3D hyperbolic space. The felicitous property that hyperbolic space has ``more room'' than Euclidean space allows more information to be seen amid less clutter, and motion by hyperbolic isometries provides for mathematically elegant navigation. The 3D graphical representations, available in the WebOOGL or VRML file formats, contain link anchors which point to the original pages on the Web itself. We use the Geomview/WebOOGL 3D Web browser as an interface between the 3D representation and the actual documents on the Web. The Web is just one example of a hierarchical tree structure with links ``back up the tree'' i.e. a directed graph which contains cycles. Our information visualization techniques are appropriate for other types of directed graphs with cycles, such as filesystems with symbolic links.
The dominant paradigm for World Wide Web navigation is pointing and clicking through traditional hypertext browsers. Clicking one's way through the Web has become very popular, but can also be very disorienting. The Web is so interconnected and huge that it is difficult to establish a mental model of its structure.
Flat one-dimensional history lists are one common navigational aid. Such lists provide a way to think about many documents at once, but offer no help in understanding the connections between them. Traditional two-dimensional Web browsers provide a way to focus on an individual document and see all of its outgoing connections, but do not show incoming links or offer an overview of more than one document at once.
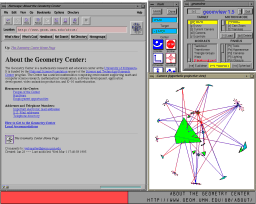
Moving up to three dimensions allows us to see both multiple documents and the links between them. The Web is far too large to see all at once, but we can explore sections of it and build 3D graphical representations which can be viewed in a 3D Web browser. Such browsers are becoming widespread with the recent release of the VRML standard. Just as traditional browsers allow one to follow links in hypertext, the VRML standard provides a way to attach three dimensional link anchors to 3D data files. The graphical representation of a document is the anchor which points to the document itself itself. Actions taken in the 3D browser can control the 2D browser and vice versa. Figure 1 shows a typical session.
Figure 1: Using the WebOOGL system for information visualization in hyperbolic space Although the Web is non-linear, we can start at any document and impose a tree structure: the chosen node is the root, each outgoing link is a first-generation child, the links in these documents are grandchildren, and so on. We construct a 3D graphical representation of a piece of this structure, drawing tetrahedra at the nodes and lines between them to represent hyperlinks. Our layout is a variant of the Xerox PARC Cone Tree [9], where the parent node is at the tip of the cone and the edges leading to the children are drawn radiating outwards to the rim.
Figure 2: Euclidean conetree, showing two levels of the 1994 Geometry Center Web The problem, as we can see in Figure 2, is that our cone trees become cluttered very quickly. There is no good way of embedding an exponentially growing tree in Euclidean space that allows us to simultaneously see both the entire structure and a closeup of a particular region.
The solution is to use hyperbolic cone trees. Hyperbolic geometry offers us an elegant way to see the big picture and the interesting details at the same time.
Mathematically consistent alternatives to Euclidean geometry have been developed over the past hundred years. The noneuclidean geometries can be distinguished by the behavior of parallel lines: in Euclidean space there is exactly one line passing through a given point which is parallel to a given line, but in hyperbolic geometry there are many. In this space the area of a circle grows exponentially with respect to its radius, whereas in Euclidean space the area only grows linearly. Thanks to this property of hyperbolic distance we have a convenient way to visualize exponentially growing trees.
The simplest way to draw 3D hyperbolic pictures is in the interior of a ball. We use Euclidean straight lines, but the way we measure distance is changed so that the surface of the ball is infinitely far away from the origin. From the outside, objects very near the center seem almost Euclidean but seem to grow distorted and smaller as they are translated towards the surface of the ball. This representation of hyperbolic space is known as the projective or Klein model. Luckily we can draw such pictures using 4 x 4 matrices: since the standard graphics pipeline uses homogeneous coordinates, interactive speeds are easily achieved on modern workstations. Figure 3 shows a navigation sequence in the projective model. The look and feel of the system is difficult to communicate with still pictures, a video is necessary to do it justice.
Figure 3: Motion in hyperbolic space (the projective model)
WebOOGL [120 KB] VRML [250 KB] MPEG [900 KB] The conformal or Poincaré model is related to the projective model by a simple transformation. In this model, straight lines are drawn as arcs and flat faces are drawn as parts of spheres. The advantage is that angles are always drawn correctly. Unfortunately we cannot use 4 x 4 matrices to represent motion in the conformal model, and drawing arcs and curved faces also requires much greater subdivision than in the projective case. While this model is more computationally demanding than the projective one, it is within the reach of most workstations.
If we allow the camera to go outside of the ball we can see the
entire space at once. When we constrain the camera itself according to
hyperbolic isometries, it can never move outside of the ball and we
see what hyperbolic space would look like from the insider's point of
view. These three models provide different and useful intuition, so we
use whichever of them is appropriate at any given time. Figure
4 shows two levels of the Geometry Center
Weblet in the three models. (We use ``Weblet'' to refer to a section
of the Web 5.) Here we have drawn the ``sphere at infinity''
for the two outsider models but in all other pictures the sphere is
not shown.
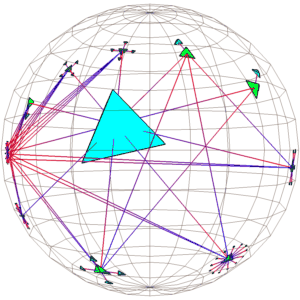
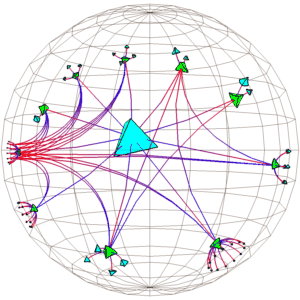
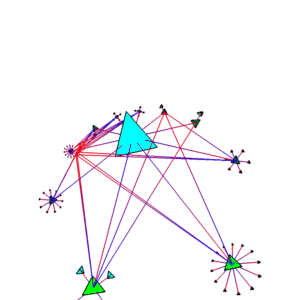
Figure 4: The projective, conformal, and ``insider'' models of hyperbolic space
MPEG projective [1.15MB] MPEG conformal [700KB] MPEG insider [360KB] There has been considerable work at the Geometry Center on visualizing hyperbolic geometry. The 1991 mathematical animation Not Knot [3] includes a groundbreaking flythrough of hyperbolic space. A reference on hyperbolic navigation can be found in [1], which to the best of our knowledge contains the first recorded suggestion of using hyperbolic space for tree visualization. See also [2] for more exposition of hyperbolic geometry aimed at the computer graphics community.
The publicly distributed Geomview 3D viewer [8] includes built-in support for interactive navigation in noneuclidean geometries, including hyperbolic geometry. Details on the implementation of the hyperbolic transformation libraries used in Geomview can be found in [7].
A recent paper from Lamping et al at Xerox PARC [4] has brought hyperbolic visualization to the attention of the computer-human interaction community. They ran user tests of a 2D Poincaré model browser visualizing various kinds of hierarchical information, including organizational charts and a Weblet. Their work on information visualization is confined to the 2D hyperbolic plane, and deals only with acyclic graphs.
Hyperbolic space has a similar visual effect to a fisheye camera lens, used by [10] for information visualization. The fisheye paradigm calls for several ad-hoc decisions, the advantage of hyperbolic geometry is it provides an elegant and powerful mathematical framework for display and navigation.
The graph can be easily laid out in the hyperbolic plane using
uniform edge lengths. Indeed, this property of hyperbolic geometry is
one of the motivations behind its use. However, we would like to
optimize our use of space so that as many generations as possible are
visible. (This optimization also forestalls a bit longer the
inevitable cumulative floating-point error). So we would like edges
that connect nodes to be as short as possible, yet we must also avoid
overlaps between the cone trees of all
future generations. In order to most economically meet these
constraints, the hyperbolic length
![]() of the edge
connecting nodes i and j should be
of the edge
connecting nodes i and j should be
When the cone tree angle (a user-specifiable parameter) is 90 degrees, cones become flat disks. While this would negate most of the advantages of cone trees in Euclidean space, in hyperbolic space disks are very convenient. The hierarchy of disks has no directional bias: locally, child nodes are indistinguishable from parent nodes. Whichever node is closest to the origin of the sphere ``feels'' like the root node.
Figure 5: Angle between edges incident on node i.
The Web is distributed resource which maintains a (very large) directed graph whose nodes are documents and whose edges are links between them (labelled by link relationships). Although it may provide a useful mental picture to think of a Weblet as tree hierarchy, most Weblets are not even directed acyclic graphs (DAGs), often containing many cycles due to ``backlinks''. Other common information hierarchies, such as a Unix filesystem with symbolic or hard links, also allow cycles.
Again hyperbolic geometry offers an elegant, systematic approach to visualizing directed graphs containing cycles. Just as trees can be nicely embedded in standard hyperbolic space (which contains no topologically significant loops), so too can directed graphs with cycles be nicely imbedded in hyperbolic manifolds--spaces which can wrap around and close up on themselves. Standing in such a space, you would be able to see many copies of yourself off in the distance, each image corresponding to one way that a light ray can loop back to you by following the wraparound topology of the space. The effect would be similar to a hall of mirrors, except that the images would never be right-left reversed. If there were a graph laid out in such a manifold, you would be able to see, receding into the distance, images of the current location which represent longer and longer chains of links leading back to that node. See [2] for more details on visualizing 3-manifolds from this ``insider's'' point of view.
However, due to the multiple images, sophisticated level-of-detail culling (beyond the abilities our first-generation software) is required to render the view inside a manifold efficiently. For this reason, we have initially taken an approach based on laying out an exhaustive subtree of the graph in standard hyperbolic space and then filling in the ``backlink'' edges (which will hopefully be as uniformly distributed as possible). The choice of an exhaustive subtree corresponds in more detail to choosing (1) a ``root node'', and (2) for each other node, one incoming edge as its ``main entry point''.
To see how to choose the entry points for best layout, consider first the (infinite) tree that would be obtained by navigating out from the root node, and attaching to each node copies of all its children, without regard to whether those children have already been seen and placed in the growing tree. This is similar to the manifold picture, but somewhat misleading as every node has multiple graphical representations, each variant missing all but one of the incoming edges. Figure 6, which shows such a layout, was made from the same data set as Figure 4. Nodes which are multiply represented are drawn in yellow.
Figure 6: No backlinks
WebOOGL [60KB] VRML [130KB] MPEG [200KB] The required subtree can now be selected by choosing a traversal order for the above tree, and then only retaining the first copy of each graph node. The choice of traversal order has a major impact on the comprehensibility of the picture. Breadth-first search starting at the root node results in a more balanced, clearer picture than depth-first search. Compare Figures 7 and 8, which show the highly connected Weblet of an index of German cities.
Figure 7: Breadth-first search
WebOOGL [200KB] VRML [300KB] MPEG [200KB]
Figure 8: Depth-first search
WebOOGL [130KB] VRML [300KB] MPEG [1.02MB]
We use an adapted version of Nierstrasz's explore perl script as a Web spider to construct a raw list of Weblet links. The adaptations include the use of the libwww-perl libraries. The C++ program that creates a graphical representation of the Weblet links with the OOGL transformation libraries [7], which support 3D hyperbolic transformations. The original Euclidean version demonstrated in 1994 was called webspace. Due to the release of the popular VRML browser by that name from SGI, we have renamed the hyperbolic version webviz.
For a 3D Web browser we use the Geomview/ WebOOGL software system. Geomview is a public domain 3D viewer which runs on SGI, X, and NeXTStep workstations. The original WebOOGL system demoed in 1994 [6] had a very different structure than the current WebOOGL 2.0 configuration. See [5] for details on the WebOOGL system.
The structure of the Web is just one of many potential applications of visualizing directed graphs with cycles. The file format expected by the webviz program can easily be generated by programs other than a Webspider. We have implemented a straightforward Unix filesystem explorer using find and perl. Figure 9 shows the directories on the SFB 288 filesystem and the symbolic links between them. The complex subtree at the lower left is /usr, the node with the most children at the upper left is /u (the index of all home directories), and the many symbolic links at the top connect NFS-mounted disks local to individual machines to the main filesystem. We would like to try visualizing other kind of information, such as object class hierarchies.
Figure 9: Filesystem visualization
WebOOGL [330KB] VRML [770KB] MPEG [380KB] The system is currently limited by rendering speed. Level of detail control will be crucial to extending its reach.
The current Webviz system is batch-oriented: the Webspider explores a Weblet to a specified depth and then the graphical representation is constructed and written out into a 3D data file. The file is then loaded into Geomview through the WebOOGL system. The current WebOOGL interface controls the click action, toggling between showing information about the node and following its link. A nice extension would be a user interface for interactive control of the Weblet exploration, where possible click actions would be collapsing or exploring nodes, selecting which backlinks to draw or hide, etc.
There are a number of possible directions for the layout. We now always avoid overlapping nodes by erring on the side of over-allocating space for the children of a node. Not only can this obscure the big picture, but also the current scheme runs into floating-point precision difficulties after several generations. (Of course, without level of detail culling we are often render-bound after three or four generations.) Distributing the child nodes on the surface of spheres instead of cones would use space more efficiently. An interesting approach would be to use the currently computed layout as the starting point for a dynamical system where the edges act as repulsive springs. The system could evolve until it converged to a solution which fits (no overlap) and fits well (each node occupies just as much space as it needs). Because of the self-similar nature of trees, this dynamical system would probably need to be applied in a hierarchical way similar to multi-grid techniques. Another interesting tactic would be to draw the backlinks as splines instead of straight lines. While splines in Euclidean space have been extensively investigated, hyperbolic splines have received much less attention.
Much more could be done to graphically represent the contents of the node. Color coding is now used to show link directionality and to crudely show the generation in the tree. For example, color coding and edge thickness could represent attributes such as document size, number of accesses, modification times, and so on. All nodes are now HTML documents and are just drawn as tetrahedra, but if the Web spider were improved to gather information for all recognized MIME types the node shape could represent the document content type.
We have implemented a system for visualizing information hierarchies, specifically directed graphs with cycles, in 3D hyperbolic space. We have used this system to construct graphical representations of the structure of the World-Wide Web and Unix filesystems. Our approach offers a seamless framework for both a visual gestalt of the entire system and closeup detail at any level of the hierarchy.
Many thanks to Charlie Gunn for his mathematical suggestions and technical advice. Thanks also to Stuart Levy for his contributions to the Webviz and WebOOGL software and Daeron Meyer for his work on WebOOGL. I would like to acknowledge Ed H. Chi for his original program which constructed a Euclidean graphical representation of a piece of the Web as shown in Figure 2.
This work was partially supported by the Geometry Center (University of Minnesota) and by the SFB288 (Technical University of Berlin). The Geometry Center is funded by the NSF (DMS-8920161) and the DOE(DOE/DE-FG02-92ER25137).