To evaluate the tolerance of the spacetime method to changes in
reflectance, we performed two experiments, one quantitative and the
other qualitative. For the first experiment, we generated planar
cards with step reflectance changes varying from about 1:1 to 10:1 and
scanned them at an angle of 
(roughly facing the sensor).
Figure 9 shows a plot of maximum deviations from
planarity when using traditional per scanline mean analysis and our
spacetime analysis. The spacetime method has clearly improved over
the old method, yielding up to 85% reductions in range errors.
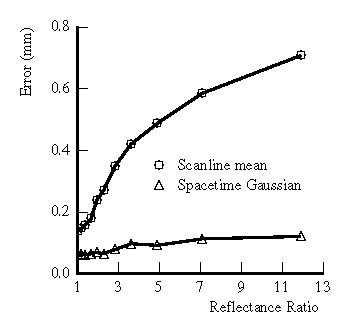
Figure 9: Measured
error due to varying reflectance steps.
For qualitative comparison, we produced a planar sheet with the word ``Reflectance'' printed on it. Figure 10 shows the results. The old method yields a surface with the characters well-embossed into the geometry, whereas the spacetime method yields a much more planar surface indicating successful decoupling of geometry and reflectance.
Figure 10: Reflectance
card. (a) Photograph of a planar card with the word ``Reflectance''
printed on it, and shaded renderings of the range data generated by
(b) mean pulse analysis and (c) spacetime analysis.
We conducted several experiments to evaluate the effects of shape variation on range acquisition. In the first experiment, we generated corners of varying angles by abutting sharp edges of machined aluminum wedges which are painted white. Figure 11 shows the range errors that result for traditional and spacetime methods. Again, we see an increase in accuracy, though not as great as in the reflectance case.
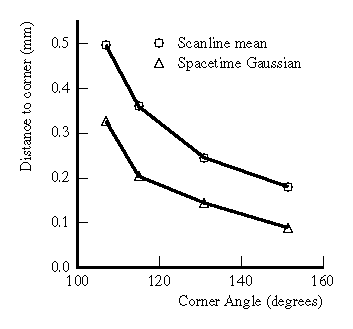
Figure 11: Measured
error due to corners of varying angles.
We also scanned two 4 mm strips of paper at an angle of
(roughly facing the sensor) to examine the effects of depth
continuity. Figure 12b shows the ``edge curl''
observed with the old method, while the spacetime method in
Figure 12c shows a significant reduction of this
artifact under spacetime analysis. We have found that the spacetime
method reduces the length of the edge curl from an average of 1.1 mm
to an average of approximately 0.35 mm.
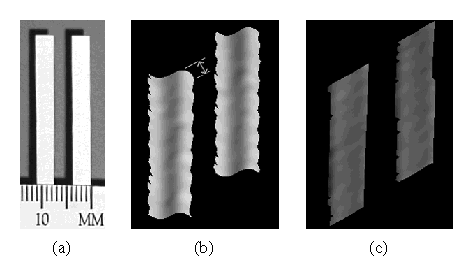
Figure 12: Depth discontinuities and
edge curl. (a) Photograph of two strips of paper, and shaded
renderings of the range data generated by (b) mean pulse analysis and
(c) spacetime analysis. The ``edge curl'' indicated by the hash-marks
in (b) is 1.1mm.
Finally, we impressed the word ``shape'' onto a plastic ribbon using a commonly available label maker. In Figure 10, we wanted the word ``Reflectance'' to disappear because it represented changes in reflectance rather than in geometry. In Figure 13, we want the word ``Shape'' to stay because it represents real geometry. Furthermore, we wish to resolve it as highly as possible. Figure 13 shows the result. Using the scanline mean method, the word is barely visible. Using the new spacetime analysis, the word becomes legible.
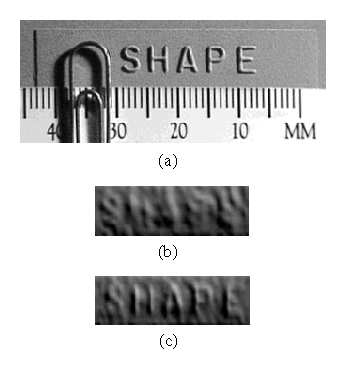
Figure 13: Shape ribbon. (a)
Photograph of a surface with raised lettering (letters are approx. 0.3
mm high), and renderings of the range data generated by (b) mean pulse
analysis and (c) spacetime analysis.
We performed range scans on the planar surfaces and generated range points using the traditional and spacetime methods. After fitting planes to range points, we found a 30-60% reduction in average deviation from planarity when using the spacetime analysis.
Figure 14 shows the results of scanning a model tractor. Figure 14b is a rendering of the data generated by the Cyberware scanner hardware and is particularly noisy. This added noisiness results from the method of pulse analysis performed by the hardware, a method similar to peak detection. Peak detection is especially susceptible to speckle noise, because it extracts a range point based on a single value or small neighborhood of values on a noisy curve. Mean analysis tends to average out the speckle noise, resulting in smoother range data as shown in Figure 14c. Figure 14d shows our spacetime results and Figure 14e shows the spacetime results with 3X interpolation and resampling of the spacetime volume as described in section 4.2. Note the sharper definition of features on the body of the tractor and less jagged edges in regions of depth discontinuity.
Figure 14:
Model tractor. (a) Photograph of original model and shaded renderings
of range data generated by (b) the Cyberware scanner hardware, (c)
mean pulse analysis, (d) our spacetime analysis, and (e) the spacetime
analysis with 3X interpolation of the spacetime volume before fitting
the Gaussians. Below each of the renderings is a blow-up of one
section of the tractor body (indicated by rectangle on rendering) with
a plot of one row of pixel intensities.
The results we presented in this section clearly show that the spacetime analysis yields more accurate range data, but the results are imperfect due to system limitations. These limitations include: