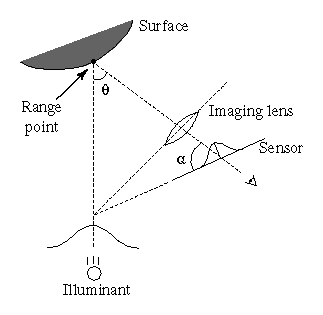
Figure 1: Optical triangulation geometry. The angle
is the triangulation angle
while 
is the tilt of the sensor plane needed to keep the
laser plane in focus.
Brian Curless and Marc Levoy
Stanford University
The standard methods for extracting range data from optical triangulation scanners are accurate only for planar objects of uniform reflectance illuminated by an incoherent source. Using these methods, curved surfaces, discontinuous surfaces, and surfaces of varying reflectance cause systematic distortions of the range data. Coherent light sources such as lasers introduce speckle artifacts that further degrade the data. We present a new ranging method based on analyzing the time evolution of the structured light reflections. Using our spacetime analysis, we can correct for each of these artifacts, thereby attaining significantly higher accuracy using existing technology. We present results that demonstrate the validity of our method using a commercial laser stripe triangulation scanner.
Active optical triangulation is one of the most common methods for acquiring range data. Although this technology has been in use for over twenty years, its speed and accuracy has increased dramatically in recent years with the development of geometrically stable imaging sensors such as CCD's and lateral effect photodiodes. The range acquisition literature contains many descriptions of optical triangulation range scanners, of which we list a handful [2] [8] [10] [12] [14] [17] . The variety of methods differ primarily in the structure of the illuminant (typically point, stripe, multi-point, or multi-stripe), the dimensionality of the sensor (linear array or CCD grid), and the scanning method (move the object or move the scanner hardware).
Figure 1 shows a typical system configuration in two dimensions. The location of the center of the reflected light pulse imaged on the sensor corresponds to a line of sight that intersects the illuminant in exactly one point, yielding a depth value. The shape of the object is acquired by translating or rotating the object through the beam or by scanning the beam across the object.
The accuracy of optical triangulation methods hinges on the ability to locate the ``center'' of the imaged pulse at each time step. For optical triangulation systems that extract range from single imaged pulses at a time, variations in surface reflectance and shape result in systematic range errors. Several researchers have observed one or both of these accuracy limitations [4] [12] [16]. For the case of coherent illumination, the images of reflections from rough surfaces are also subject to laser speckle noise, introducing noise into the range data. Researchers have studied the effect of speckle on range determination and have indicated that it is a fundamental limit to the accuracy of laser range triangulation, though its effects can be reduced with well-known speckle reduction techniques [1] [5]. Mundy and Porter [12] attempt to correct for variations in surface reflectance by noting that two imaged pulses, differing in position or wavelength are sufficient to overcome the reflectance errors, though some restrictive assumptions are necessary for the case of differing wavelengths. Kanade, et al, [11] describe a rangefinder that finds peaks in time for a stationary sensor with pixels that view fixed points on an object. This method of peak detection is very similar to the one presented in this paper for solving some of the problems of optical triangulation; however, the authors in [11] do not indicate that their design solves or even addresses these problems. Further, we show that the principle generalizes to other scanning geometries.
In the following sections, we first show how range errors arise with traditional triangulation techniques. In section 3, we show that by analyzing the time evolution of structured light reflections, a process we call spacetime analysis, we can overcome the accuracy limitations caused by shape and reflectance variations. Experimental evidence also indicates that laser speckle behaves in a manner that allows us to reduce its distorting effect as well.
In sections 4 and 5, we describe our hardware and software implementation of the spacetime analysis using a commercial scanner and a video digitizer, and we demonstrate a significant improvement in range accuracy. Finally, in section 6, we conclude and describe future directions.
Figure 1: Optical
triangulation geometry. The angle is the triangulation angle
while is the tilt of the sensor plane needed to keep the
laser plane in focus.
For optical triangulation systems, the accuracy of the range data depends on proper interpretation of imaged light reflections. The most common approach is to reduce the problem to one of finding the ``center'' of a one dimensional pulse, where the ``center'' refers to the position on the sensor which hopefully maps to the center of the illuminant. Typically, researchers have opted for a statistic such as mean, median or peak of the imaged light as representative of the center. These statistics give the correct answer when the surface is perfectly planar, but they are generally inaccurate whenever the surface perturbs the shape of the illuminant.
Perturbations of the shape of the imaged illuminant occur whenever:
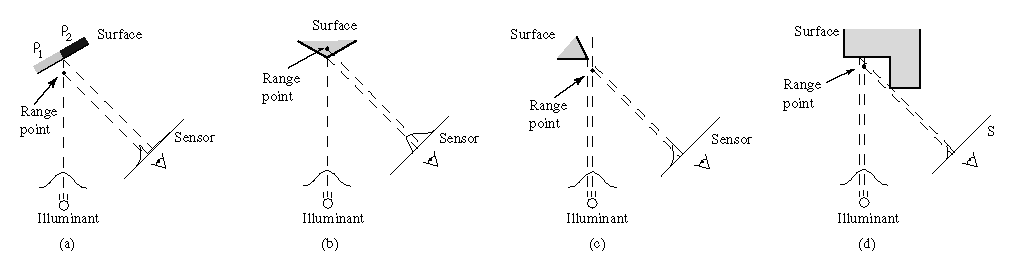
Figure 2: Range errors
using traditional triangulation methods. (a) Reflectance
discontinuity. (b) Corner. (c) Shape discontinuity with respect to
the illumination. (d) Sensor occlusion.
The fourth source of range error is laser speckle, which arises when coherent laser illumination bounces off of a surface that is rough compared to a wavelength [7]. The surface roughness introduces random variations in optical path lengths, causing a random interference pattern throughout space and at the sensor. The result is an imaged pulse with a noise component that affects the mean pulse detection, causing range errors even from a planar target.
To quantify the errors inherent in using mean pulse analysis, we have
computed the errors introduced by reflectance and shape variations for
an ideal triangulation system with a single Gaussian illuminant. We
take the beam width, w, to be the distance between the beam center
and the 
point of the irradiance profile, a convention common
to the optics literature. We present the range errors in a scale
invariant form by dividing all distances by the beam width.
Figure 3 illustrates the maximum deviation from
planarity introduced by scanning reflectance discontinuities of
varying step magnitudes for varying triangulation angles. As the size
of the step increases, the error increases correspondingly. In
addition, smaller triangulation angles, which are desirable for
reducing the likelihood of missing data due to sensor occlusions,
actually result in larger range errors. This result is not
surprising, as sensor mean positions are converted to depths through a
division by 
, where is the triangulation angle, so
that errors in mean detection translate to larger range errors for
smaller triangulation angles.
Figure 4 shows the effects of a corner on
range error, where the error is taken to be the shortest distance
between the computed range data and the exact corner point. The
corner is oriented so that the illumination direction bisects the
corner's angle as shown in Figure 2b. As we
might expect, a sharper corner results in greater compression of the
left side of the imaged Gaussian relative to the right side, pushing
the mean further to the right on the sensor and pushing the
triangulated point further behind the corner. In this case, the
triangulation angle has little effect as the division by
is offset almost exactly by the smaller observed left/right pulse
compression imbalance.
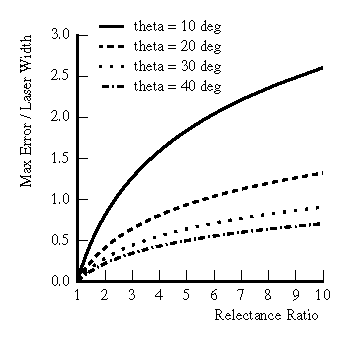
Figure 3: Plot of
errors due to reflectance discontinuities for varying triangulation
angles (theta).
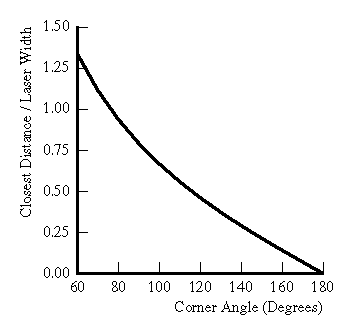
Figure 4: Plot of
errors due to corners.
One possible strategy for reducing these errors would be to decrease the width of the beam and increase the resolution of the sensor. However, diffraction limits prevent us from focusing the beam to an arbitrary width. The limits on focusing a Gaussian beam with spherical lenses are well known [15]. In recent years, Bickel, et al, [3] have explored the use of axicons (e.g., glass cones and other surfaces of revolution) to attain tighter focus of a Gaussian beam. The refracted beam, however, has a zeroth order Bessel function cross-section; i.e., it has numerous side-lobes of non-negligible irradiance. The influence of these side-lobes is not well-documented and would seem to complicate triangulation.
The previous section clearly demonstrates that analyzing each imaged pulse using a low order statistic leads to systematic range errors. We have found that these errors can be reduced or eliminated by analyzing the time evolution of the pulses.
Figure 5 illustrates the principle of spacetime
analysis for a laser triangulation scanner with Gaussian illuminant
and orthographic sensor as it translates across the edge of an object.
As the scanner steps to the right, the sensor images a smaller and
smaller portion of the laser cross-section. By time 
, the sensor
no longer images the center of the illuminant, and conventional
methods of range estimation fail. However, if we look along the lines
of sight from the corner to the laser and from the corner to the
sensor, we see that the profile of the laser is being imaged over
time onto the sensor (indicated by the dotted Gaussian envelope).
Thus, we can find the coordinates of the corner point 
by
searching for the mean of a Gaussian along a constant line of sight
through the sensor images. We can express the coordinates of this
mean as a time and a position on the sensor, where the time is in
general between sensor frames and the position is between sensor
pixels. The position on the sensor indicates a depth, and the time
indicates the lateral position of the center of the illuminant. In
the example of Figure 5, we find that the spacetime
Gaussian corresponding to the exact corner has its mean at position
on the sensor at a time 
between 
and during the
scan. We extract the corner's depth by triangulating the center of
the illuminant with the line of sight corresponding to the sensor
coordinate , while the corner's horizontal position is
proportional to the time .
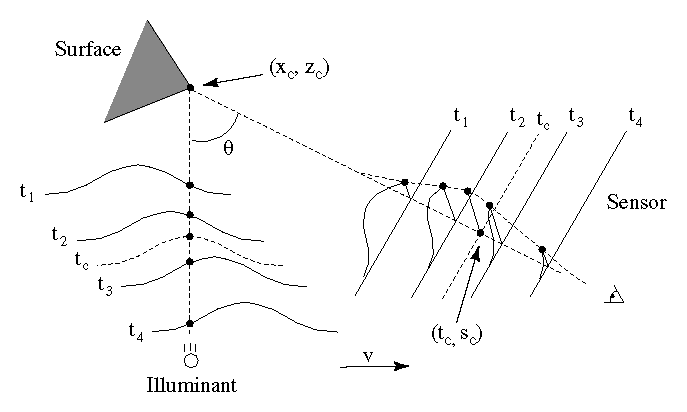
Figure 5: Spacetime mapping of a Gaussian
illuminant. As the light sweeps across the corner point, the
sensor images the shape of the illuminant over time.
For a more rigorous analysis, we consider the time evolution of the
irradiance from a translating differential surface element, 
,
as recorded at the sensor. We refer the reader to
Figure 6 for a description of coordinate systems;
note that in contrast to the previous section, the surface element is
translating instead of the illuminant-sensor assembly.
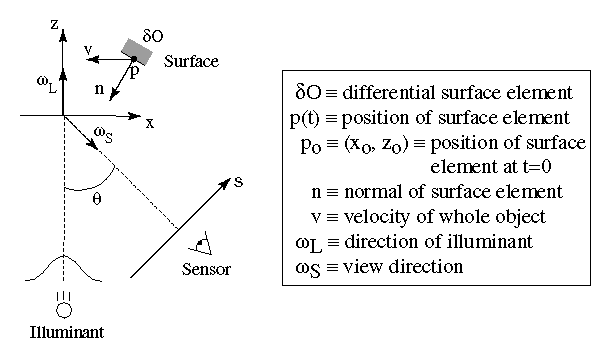
Figure 6: Triangulation scanner coordinate
system. A depiction of the coordinate systems and the vectors
relevant to a moving differential element.
The element has a normal 
and an initial position 
and is translating with velocity 
, so that:
Our objective is to compute the coordinates 
given the temporal irradiance variations on the sensor. For
simplicity, we assume that 
. The illuminant we
consider is a laser with a unidirectional Gaussian radiance profile.
We can describe the total radiance reflected from the element to the
sensor as:
where 
is the bidirectional reflection distribution function
(BRDF) of the point , 
is
the cosine of the angle between the surface and illumination. The
remaining terms describe a point moving in the x-direction under the
Gaussian illuminant of width w and power 
.
Projecting the point 
onto the sensor, we find:
where s is the position on the sensor and is the angle
between the sensor and laser directions. We combine
Equations 2-3 to give us an equation
for the irradiance observed at the sensor as a function of time and
position on the sensor:
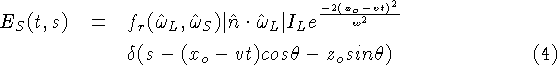
To simplify this expression, we condense the light reflection terms into one measure:
which we will refer to as the reflectance coefficient of point
for the given illumination and viewing directions. We also
note that x=vt is a measure of the relative x-displacement of the
point during a scan, and 
is the relation between
sensor coordinates and depth values along the center of the
illuminant. Making these substitutions we have:
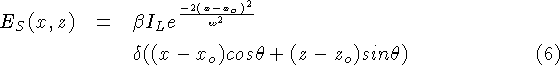
This equation describes a Gaussian running along a tilted line
through the spacetime sensor plane or ``spacetime image''. We define
the ``spacetime image'' to be the image whose columns are filled with
sensor scanlines that evolve over time. Through the substitutions
above, position within a column of this image represents displacement
in depth, and position within a row represents time or displacement in
lateral position. Figure 7 shows the theoretical
spacetime image of a single point based on the derivation above, while
Figures 8a and
8b shows the spacetime image generated
during a real scan. From Figure 7, we see that
the tilt angle is 
with respect to the z-axis, and the
width of the Gaussian along the line is:
The peak value of the Gaussian is 
, and its mean along the
line is located at 
, the exact location of the range
point. Note that the angle of the line and the width of the Gaussian
are solely determined by the fixed parameters of the scanner,
not the position, orientation, or BRDF of the surface element.
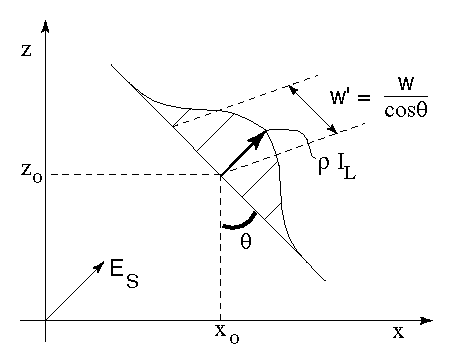
Figure 7: Spacetime image of
a point passing through a Gaussian illuminant.
Thus, extraction of range points should proceed by computing low order statistics along tilted lines through the sensor spacetime image, rather than along columns (scanlines) as in the conventional method. As a result, we can determine the position of the surface element independently of the orientation and BRDF of the element and independently of any other nearby surface elements. In theory, the decoupling of range determination from local shape and reflectance is complete. In practice, optical systems and sensors have filtering and sampling properties that limit the ability to resolve neighboring points. In Figure 8d, for instance, the extracted edges extend slightly beyond their actual bounds. We attribute this artifact to filtering which blurs the exact cutoffs of the edges into neighboring pixels in the spacetime image, causing us to find additional range values.
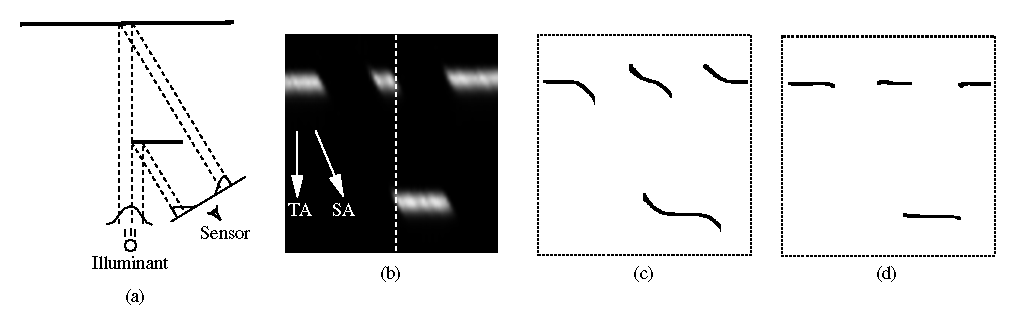
Figure 8: From geometry to spacetime image to range data. (a) The original
geometry. (b) The resulting spacetime image. TA indicates the
direction of traditional analysis, while SA is the direction of the
spacetime analysis. The dotted line corresponds to the scanline
generated at the instant shown in (a). (c) Range data after
traditional mean analysis. (d) Range data after spacetime analysis.
As a side effect of the spacetime analysis, the peak of the Gaussian yields the irradiance at the sensor due to the point. Thus, we automatically obtain an intensity image precisely registered to the range image.
We can easily generalize the previous results to other scanner geometries under the following conditions:
,
is constant. Note that the illumination need only be directional;
coherent or incoherent light of any pattern is acceptable. Further,
the translational motion need not be of constant speed, only constant
direction; we can correct for known variations in speed by applying a
suitable warp to the spacetime image.
We can weaken each of these restrictions if 
does not vary
appreciably for each point as it passes through the illuminant. A
perspective sensor is suitable if the changes in viewing directions
are relatively small for neighboring points inside the illuminant.
This assumption of ``local orthography'' has yielded excellent results
in practice. In addition, we can tolerate a rotational component to
the motion as long as the radius of curvature of the point path is
large relative to the beam width, again minimizing the effects on
.
The discussion in sections 3.1-3.3 show how we can go about extracting accurate range data in the presence of shape and reflectance variations, as well as occlusions. But what about laser speckle? Empirical observation of the time evolution of the speckle pattern with our optical triangulation scanner strongly suggests that the image of laser speckle moves as the surface moves. The streaks in the spacetime image of Figure 8b correspond to speckle noise, for the object has uniform reflectance and should result in a spacetime image with uniform peak amplitudes. These streaks are tilted precisely along the direction of the spacetime analysis, indicating that the speckle noise adheres to the surface of the object and behaves as a noisy reflectance variation. Other researchers have observed a ``stationary speckle'' phenomenon as well [1]. Proper analysis of this problem is an open question, likely to be resolved with the study of the governing equations of scalar diffraction theory for imaging of a rough translating surface under coherent Gaussian beam illumination [6].
We have implemented the spacetime analysis presented in the previous section using a commercial laser triangulation scanner and a real-time digital video recorder.
The optical triangulation system we use is a Cyberware MS platform
scanner. This scanner collects range data by casting a laser stripe
on the object and by observing reflections with a CCD camera
positioned at an angle of 
with respect to the plane of the
laser. The platform can either translate or rotate an object through
the field of view of the triangulation optics. The laser width varies
from 0.8 mm to 1.0 mm over the field of view which is approximately 30
cm in depth and 30 cm in height. Each CCD pixel images a portion of
the laser plane roughly 0.5 mm by 0.5 mm. Although the Cyberware
scanner performs a form of peak detection in real time, we require the
actual video frames of the camera for our analysis. We capture these
frames with an Abekas A20 video digitizer and an Abekas A60 digital
video disk, a system that can acquire 486 by 720 size frames at 30 Hz.
These captured frames have approximately the same resolution as the
Cyberware range camera, though they represent a resampling of the
reconstructed CCD output.
Using the principles of section 3, we can devise a procedure for extracting range data from spacetime images:
.In step 2, we rotate the spacetime images so that Gaussians are vertically aligned. In a practical system with different sampling rates in x and z, the correct rotation angle can be computed as:
where is the new rotation angle, 
and 
are
the sample spacing in x and z respectively, and 
is the
triangulation angle. In order to determine the rotation angle,
, for a given scanning rate and region of the field of view of
our Cyberware scanner, we first determined the local triangulation
angle and the sample spacings in depth (z) and lateral position
(x). Equation 8 then yields the desired angle.
In step 3, we compute the statistics of the Gaussians along each rotated spacetime image raster. Our method of choice for computing these statistics is a least squares fit of a parabola to the log of the data. We have experimented with fitting the data directly to Gaussians using the Levenberg-Marquardt non-linear least squares algorithm [13], but the results have been substantially the same as the log-parabola fits. The Gaussian statistics consist of a mean, which corresponds to a range point, as well as a width and a peak amplitude, both of which indicate the reliability of the data. Widths that are far from the expected width and peak amplitudes near the noise floor of the sensor imply unreliable data which may be down-weighted or discarded during later processing (e.g., when combining multiple range meshes [18]). For the purposes of this paper, we discard unreliable data.
Finally, in step 4, we rotate the range points back into the global coordinate system.
Traditionally, researchers have extracted range data at sampling rates corresponding to one range point per sensor scanline per unit time. Interpolation of shape between range points has consisted of fitting primitives (e.g., linear interpolants like triangles) to the range points. Instead, we can regard the spacetime volume as the primary source of information we have about an object. After performing a real scan, we have a sampled representation of the spacetime volume, which we can then reconstruct to generate a continuous function. This function then acts as our range oracle, which we can query for range data at a sampling rate of our choosing. In practice, we can magnify the sampled spacetime volume prior to applying the range imaging steps described above. The result is a range grid with a higher sampling density based directly on the imaged light reflections.
To evaluate the tolerance of the spacetime method to changes in
reflectance, we performed two experiments, one quantitative and the
other qualitative. For the first experiment, we generated planar
cards with step reflectance changes varying from about 1:1 to 10:1 and
scanned them at an angle of (roughly facing the sensor).
Figure 9 shows a plot of maximum deviations from
planarity when using traditional per scanline mean analysis and our
spacetime analysis. The spacetime method has clearly improved over
the old method, yielding up to 85% reductions in range errors.
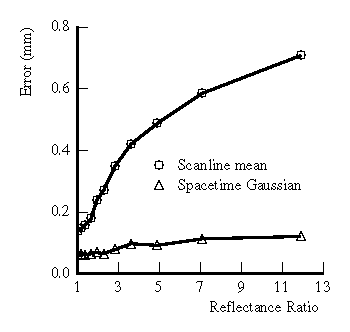
Figure 9: Measured
error due to varying reflectance steps.
For qualitative comparison, we produced a planar sheet with the word ``Reflectance'' printed on it. Figure 10 shows the results. The old method yields a surface with the characters well-embossed into the geometry, whereas the spacetime method yields a much more planar surface indicating successful decoupling of geometry and reflectance.
Figure 10: Reflectance
card. (a) Photograph of a planar card with the word ``Reflectance''
printed on it, and shaded renderings of the range data generated by
(b) mean pulse analysis and (c) spacetime analysis.
We conducted several experiments to evaluate the effects of shape variation on range acquisition. In the first experiment, we generated corners of varying angles by abutting sharp edges of machined aluminum wedges which are painted white. Figure 11 shows the range errors that result for traditional and spacetime methods. Again, we see an increase in accuracy, though not as great as in the reflectance case.
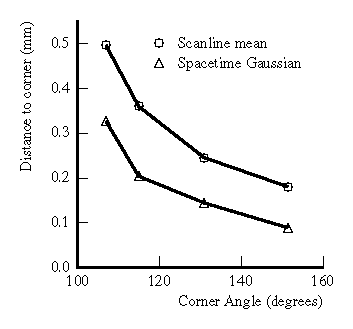
Figure 11: Measured
error due to corners of varying angles.
We also scanned two 4 mm strips of paper at an angle of
(roughly facing the sensor) to examine the effects of depth
continuity. Figure 12b shows the ``edge curl''
observed with the old method, while the spacetime method in
Figure 12c shows a significant reduction of this
artifact under spacetime analysis. We have found that the spacetime
method reduces the length of the edge curl from an average of 1.1 mm
to an average of approximately 0.35 mm.
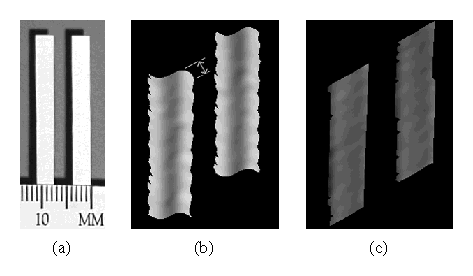
Figure 12: Depth discontinuities and
edge curl. (a) Photograph of two strips of paper, and shaded
renderings of the range data generated by (b) mean pulse analysis and
(c) spacetime analysis. The ``edge curl'' indicated by the hash-marks
in (b) is 1.1mm.
Finally, we impressed the word ``shape'' onto a plastic ribbon using a commonly available label maker. In Figure 10, we wanted the word ``Reflectance'' to disappear because it represented changes in reflectance rather than in geometry. In Figure 13, we want the word ``Shape'' to stay because it represents real geometry. Furthermore, we wish to resolve it as highly as possible. Figure 13 shows the result. Using the scanline mean method, the word is barely visible. Using the new spacetime analysis, the word becomes legible.
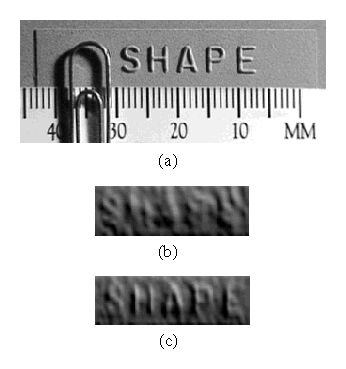
Figure 13: Shape ribbon. (a)
Photograph of a surface with raised lettering (letters are approx. 0.3
mm high), and renderings of the range data generated by (b) mean pulse
analysis and (c) spacetime analysis.
We performed range scans on the planar surfaces and generated range points using the traditional and spacetime methods. After fitting planes to range points, we found a 30-60% reduction in average deviation from planarity when using the spacetime analysis.
Figure 14 shows the results of scanning a model tractor. Figure 14b is a rendering of the data generated by the Cyberware scanner hardware and is particularly noisy. This added noisiness results from the method of pulse analysis performed by the hardware, a method similar to peak detection. Peak detection is especially susceptible to speckle noise, because it extracts a range point based on a single value or small neighborhood of values on a noisy curve. Mean analysis tends to average out the speckle noise, resulting in smoother range data as shown in Figure 14c. Figure 14d shows our spacetime results and Figure 14e shows the spacetime results with 3X interpolation and resampling of the spacetime volume as described in section 4.2. Note the sharper definition of features on the body of the tractor and less jagged edges in regions of depth discontinuity.
Figure 14:
Model tractor. (a) Photograph of original model and shaded renderings
of range data generated by (b) the Cyberware scanner hardware, (c)
mean pulse analysis, (d) our spacetime analysis, and (e) the spacetime
analysis with 3X interpolation of the spacetime volume before fitting
the Gaussians. Below each of the renderings is a blow-up of one
section of the tractor body (indicated by rectangle on rendering) with
a plot of one row of pixel intensities.
The results we presented in this section clearly show that the spacetime analysis yields more accurate range data, but the results are imperfect due to system limitations. These limitations include:
We have described several of the systematic limitations in traditional methods of range acquisition with optical triangulation range scanners, including intolerance to reflectance and shape changes and speckle noise. By analyzing the time evolution of the reflected light imaged onto the sensor, we have shown that distortions induced by shape and reflectance changes can be corrected, while the influence of laser speckle can be reduced. In practice, we have demonstrated that we can significantly reduce range distortions with existing hardware. Although the spacetime method does not completely eliminate range artifacts in practice, it has proven to reduce the artifacts in all experiments we have conducted.
In future work, we plan to incorporate the improved range data with algorithms that integrate partial triangulation scans into complete, unified meshes. We expect this improved data to ease the process of estimating topology, especially in areas of high curvature which are prone to edge curl artifacts. We will also investigate methods for increasing the resolution of the existing hardware by registering and deblurring multiple spacetime images [9]. Finally, we hope to apply the results of scalar diffraction theory to put the achievement of speckle reduction on sound theoretical footing.
We thank the people of Cyberware for the use of the range scanner and for their help in accessing the raw video output from the range camera.
Better Optical Triangulation through Spacetime Analysis
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -dir /usr/tmp/st -show_section_numbers -address [email protected] -split 0 paper.tex.
The translation was initiated by Brian Curless on Sun Sep 8 11:41:40 PDT 1996
