Camera Calibration:
We model a camera as a pin-hole device, that projects the 3-dimensional world onto a 2-dimensional image plane. The parameters we need to calibrate are the position (3 parameters) of the pinhole, the orientation of the image plane (3 degrees of rotation) and four internal parameters that define the geometry of the pinhole with respect to the image plane. They describe the focal length of the camera and the offset of the optical axis from the center of the image. Since a real camera with a lens is not exactly a pinhole device, we should also model the "distortion" caused by a lens to varying degrees of precision.All experimental techniques for calibrating a camera begin with photographing an object of known geometry with the camera to be calibrated. The idea is to get a number of correspondences between points in the world whose position (ie 3-d coordinates) are known, and the pixel coordinates of their image in the camera. Each world coordinates - pixel coordinates pair gives us one equation in terms of the camera parameters. The system of equations is solved for the camera parameters that give a "best fit" solution, by a nonlinear minimization of an error function.
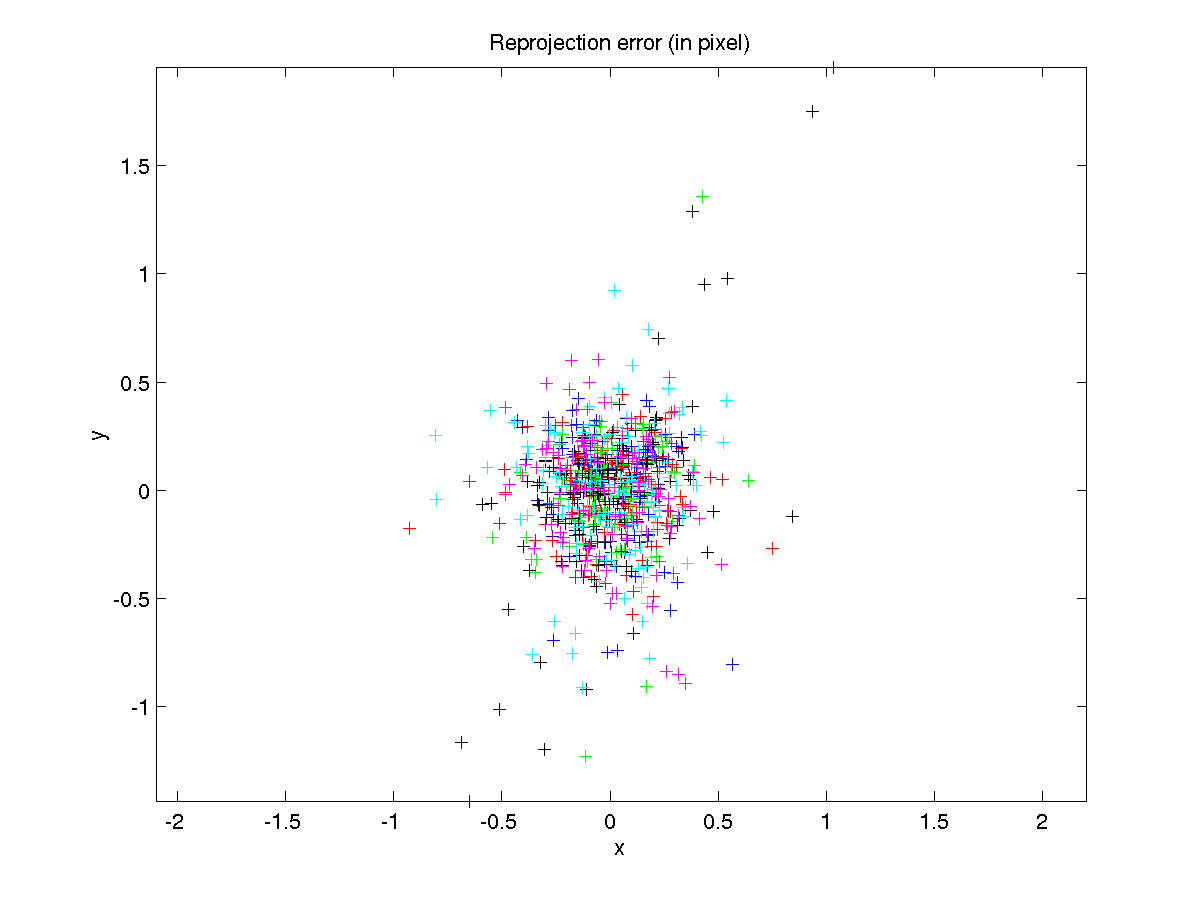
The calibration software [2, 3] we use reads the images of the calibration grid acquired
by a single camera and estimates the optimal values of camera parameters by minimizing a nonlinear error
function. We use this to calibrate each camera in our array, independent of the others. But this has some
obvious drawbacks:
We would like to implement a calibration system that tries to resolve these issues.
The Curent System:
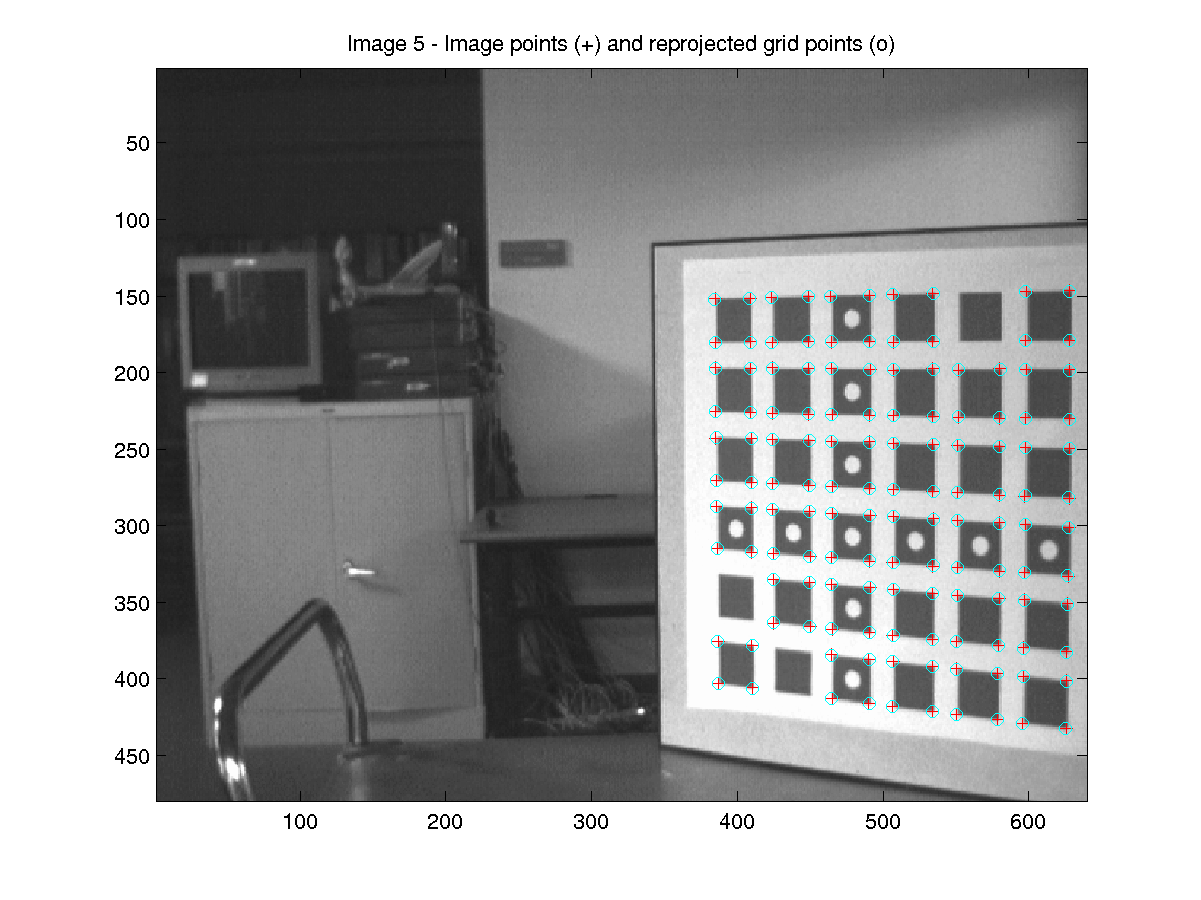
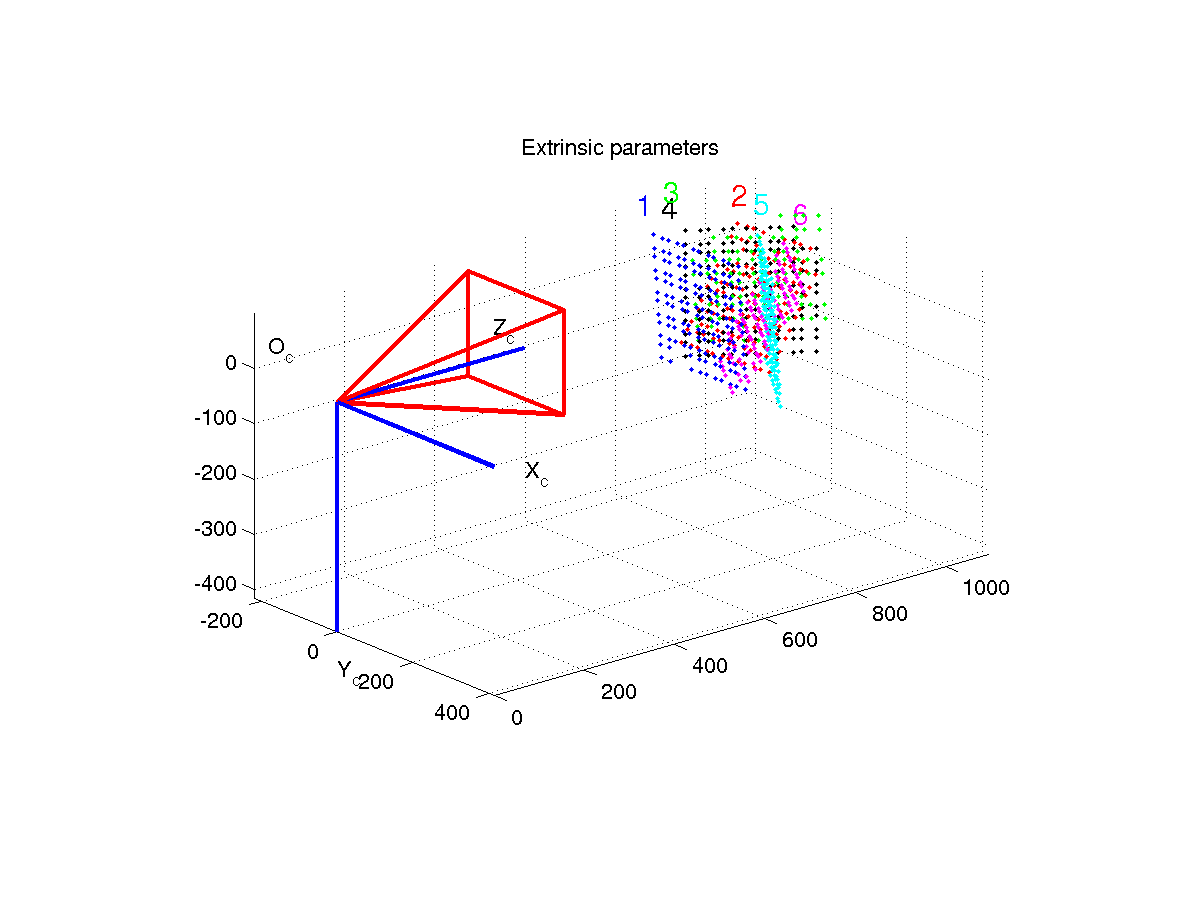
We use a plane with a patterned grid of known geometry to calibrate the cameras. The calibration procedure
involves placing the grid before the cameras in several different orientations. All cameras take a picture
of the grid for each orientation we place it in. The more the orientations in which the grid is photographed,
the more the equations we get for the camera parameters. Each equation describes the relation between a
feature point on the claibration grid, and the pixel coordinates of its image in the camera.