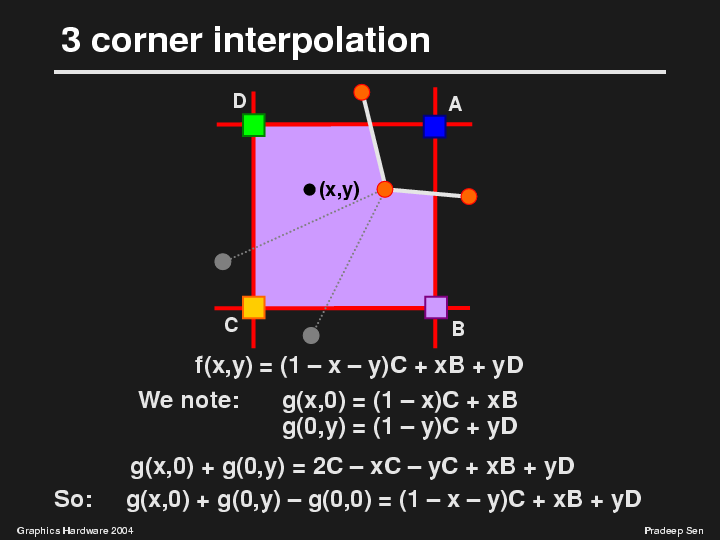
So how do we implement this function? We note that we have two linear interpolators available to us through the bilinear interpolation function g(x,y). The first is the linear interpolation between C and B, which we get if we simply plug in the x-coordinate into g(x,y) and zero out the y input. The second is the linear interpolation between C and D that can be computed if we keep the y-coordinate of the bilinear interpolation function and zero out the x input.
Now we note that if we add these two functions, we get an expression that is very similar to what we want, except that it has an extra "C" term. Thus, we can subtract out the "C" term (in this case by subtracting out g(0,0) since the origin of the cell is defined to be the C corner) to get the expression we want, f(x,y).
This means that it is possible to express the 3-corner case in terms of a combination of 3 bilinear interpolations.