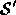 and
and 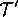 . This can be done by devising an
appropriate
. This can be done by devising an
appropriate 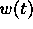 .
.
In order to obtain smoothly progressing renderings, we would like to
compensate for the exponential dependence of rendered color on opacity
as we blend 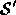 and
and 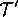 . This can be done by devising an
appropriate
. This can be done by devising an
appropriate 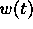 .
.
In principle, there cannot exist an ideal compensating 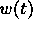 . The
exact relationship between rendered color and opacity depends on the
distance the ray travels through voxels with this opacity. Hence a
globally applied
. The
exact relationship between rendered color and opacity depends on the
distance the ray travels through voxels with this opacity. Hence a
globally applied 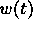 cannot compensate at once for all mismatches
since they have different thickness. Even a locally chosen
cannot compensate at once for all mismatches
since they have different thickness. Even a locally chosen 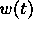 cannot work, as different viewpoints cast different rays through the
morph.
cannot work, as different viewpoints cast different rays through the
morph.
In practice, the mismatches between 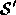 and
and 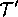 are
small in number and extent. Hence, the above theoretical objections do
not prevent us from empirically deriving a successful
are
small in number and extent. Hence, the above theoretical objections do
not prevent us from empirically deriving a successful 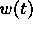 . Our
design goal is to compensate for the exponential relation of rendered
color to opacity by interpolating opacities at the rate of an inverse
exponential. The sigmoid curve given by
. Our
design goal is to compensate for the exponential relation of rendered
color to opacity by interpolating opacities at the rate of an inverse
exponential. The sigmoid curve given by
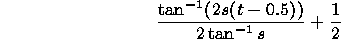
satisfies this requirement. It suppresses the contribution of
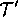 's opacity in the early part of the morph, the degree of
suppression controlled by the blending parameter
s. Similarly, the contribution of
's opacity in the early part of the morph, the degree of
suppression controlled by the blending parameter
s. Similarly, the contribution of 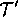 's opacity is enhanced
in the latter part of the morph. Figure 5h,
illustrates the application of compensated interpolation to the morph
of figure 5: in contrast to
figure 5g,
figure 5h looks very much like the human
head, as an early frame in the morph sequence should.
's opacity is enhanced
in the latter part of the morph. Figure 5h,
illustrates the application of compensated interpolation to the morph
of figure 5: in contrast to
figure 5g,
figure 5h looks very much like the human
head, as an early frame in the morph sequence should.